MECÂNICA GRACELI GENERALIZADA - QUÂNTICA TENSORIAL DIMENSIONAL RELATIVISTA DE CAMPOS [914]

MECÂNICA GRACELI GENERALIZADA - QUÂNTICA TENSORIAL DIMENSIONAL RELATIVISTA DE CAMPOS.

MECÃNICA GRACELI GERAL - QTDRC.

$equação Graceli dimensional relativista tensorial quântica de campos$

$\psi ^{*}$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

[

$\psi ^{*}$

$TeoriaInteraçãomediadorMagnitude relativaComportamentoFaixaCromodinâmicaForça nuclear forteGlúon10411/r71,4 × 10-15 mEletrodinâmicaForça eletromagnéticaFóton10391/r2infinitoFlavordinâmicaForça nuclear fracaBósons W e Z10291/r5 até 1/r710-18 mGeometrodinâmicaForça gravitacionalgráviton101/r2infinito$

Teoria	Interação	mediador	Magnitude relativa	Comportamento	Faixa
Cromodinâmica	Força nuclear forte	Glúon	1041	1/r7	1,4 × 10-15 m
Eletrodinâmica	Força eletromagnética	Fóton	1039	1/r2	infinito
Flavordinâmica	Força nuclear fraca	Bósons W e Z	1029	1/r5 até 1/r7	10-18 m
Geometrodinâmica	Força gravitacional	gráviton	10	1/r2	infinito

$G* = OPERADOR DE DIMENSÕES DE GRACELI.$

DIMENSÕES DE GRACELI SÃO TODA FORMA DE TENSORES, ESTRUTURAS, ENERGIAS, ACOPLAMENTOS, , INTERAÇÕES E CAMPOS, DISTRIBUIÇÕES ELETRÔNICAS, ESTADOS FÍSICOS, ESTADOS QUÂNTICOS, ESTADOS FÍSICOS DE ENERGIAS DE GRACELI, E OUTROS.

/ $\psi ^{*}$ [ $\psi ^{*}$

MECÂNICA GRACELI GENERALIZADA - QUÂNTICA TENSORIAL DIMENSIONAL RELATIVISTA DE CAMPOS. EM :

Partículas rápidas carregadas movendo-se através da matéria interagem com os elétrons dos átomos no material. A interação excita ou ioniza os átomos. Isso leva a uma perda de energia das partículas em movimento. A fórmula de Bethe descreve^[1] a média da perda de energia por distância percorrida das partículas carregadas (prótons, partículas alfa, íons atômicos, mas não elétrons^{[Footnote 1]}) atravessando a matéria (ou, alternativamente, o "poder de parada" do material). A versão não-relativística foi encontrada por Hans Bethe, em 1930; a versão relativística (abaixo) foi encontrada por ele em 1932.^[2] A perda de energia mais provável difere da perda de energia média, e é descrita pela distribuição de Landau-Vavilove.^[3]

A fórmula de Bethe é, eventualmente, chamada de "Bethe-Bloch fórmula", mas isso é enganoso (ver abaixo).

A fórmula[editar | editar código-fonte]

Para uma partícula com velocidade v, carga z (em múltiplos da carga do elétron), e energia E, viajando a uma distância x na direção de um alvo composto de elétrons de densidade numérica n e potencial médio de excitação I, a versão relativística da fórmula lida em unidades do SI é:^[2]

$-\left\langle {\frac {dE}{dx}}\right\rangle ={\frac {4\pi }{m_{e}c^{2}}}\cdot {\frac {nz^{2}}{\beta ^{2}}}\cdot \left({\frac {e^{2}}{4\pi \varepsilon _{0}}}\right)^{2}\cdot \left[\ln \left({\frac {2m_{e}c^{2}\beta ^{2}}{I\cdot (1-\beta ^{2})}}\right)-\beta ^{2}\right]$ , (1) / $\psi ^{*}$ [ $\psi ^{*}$

onde c é a velocidade da luz e ε₀, a permissividade do vácuo, $\beta ={\frac {v}{c}}$ , e e m_e, respectivamente, a carga do elétron e a massa de repouso.

O Poder de parada de Alumínio para Prótons versus prótons de energia, e a fórmula de Bethe sem (vermelho) e com correções (azul)

Aqui, a densidade numérica de elétrons do material pode ser calculada por

n={\frac {N_{A}\cdot Z\cdot \rho }{A\cdot M_{u}}}\,,

/ $\psi ^{*}$ [ $\psi ^{*}$

onde ρ é a densidade do material; Z, seu número atômico; A, sua massa atômica relativa; N_A, o número de Avogadro e M_u, a massa Molar constante.

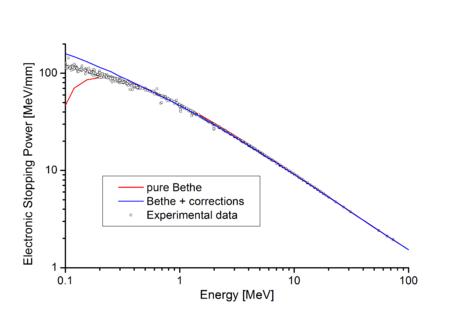
Na figura à direita, os pequenos círculos são resultados experimentais obtidos a partir de medições de vários cientistas, enquanto que a curva vermelha é a fórmula de Bethe.^[4] Evidentemente, a teoria de Bethe concorda muito bem com experiência em alta energia. A concordância é melhor ainda quando as correções são aplicadas (ver abaixo).

Para baixas energias, por exemplo, para pequenas velocidades das partículas β << 1, a fórmula de Bethe se reduz a

$-{\frac {dE}{dx}}={\frac {4\pi nz^{2}}{m_{e}v^{2}}}\cdot \left({\frac {e^{2}}{4\pi \varepsilon _{0}}}\right)^{2}\cdot \left[\ln \left({\frac {2m_{e}v^{2}}{I}}\right)\right].$

(2)

Isso pode ser visto substituindo ßc por v na eq. (1) e, em seguida, negligenciando β² devido ao seu pequeno tamanho.

Portanto, em baixas energias, a perda de energia de acordo com a fórmula de Bethe diminui aproximadamente como v^-2 com o aumento da energia. Ela atinge um mínimo em, aproximadamente, E = 3Mc², onde M é a massa da partícula (para prótons, seria algo em torno de 3000 MeV). Para muitos casos relativísticos β ≈ 1, a perda de energia aumenta novamente, mas de forma logarítmica devido à componente transversal do campo elétrico.

O potencial médio de excitação[editar | editar código-fonte]

Na teoria de Bethe, o material é completamente descrito por um único número, o potencial médio de excitação I. Em 1933, Felix Bloch mostrou que a média do potencial de ionização dos átomos é aproximadamente dada por:

I = (10 eV) . Z, (3) / $\psi ^{*}$ [ $\psi ^{*}$

onde Z é o número atômico dos átomos do material. Se esta aproximação é introduzida na fórmula (1) acima, obtém-se uma expressão que é muitas vezes chamadoa de Bethe-Bloch fórmula. Mas desde que nós temos agora tabelas com valores precisos de I como uma função de Z (ver abaixo), podemos usá-las para obter melhores resultados do que a utilização da fórmula (3).

A figura mostra valores normalizados de I, tomados a partir de uma tabela.^[5] Os picos e vales na figura levam a correspondentes vales e picos no "poder de parada". Estes são chamados de "Z₂-oscilações" ou "Z₂-estrutura" (onde Z₂ = Z significa o número atômico do alvo).

Pesquisar este blog

MECÂNICA GRACELI GENERALIZADA - QUÂNTICA TENSORIAL DIMENSIONAL RELATIVISTA DE CAMPOS [914]

A fórmula[editar | editar código-fonte]

O potencial médio de excitação[editar | editar código-fonte]

Comentários

Postar um comentário